HOMEWORK 2

DUE: Monday, February 4

 

 

1. In Homework 1, we evaluated the isothermal compressibility, k = 1/P, for an ideal gas.

 

                                                  

  

For a liquid, k is approximately constant.

 

a) Show that a liquid can be compressed from an initial state P0, V0  under a pressure P to a final volume, V, given by:

 

                                     

 

b) Calculate the reversible work for this compression.

 

(Hint: use     )

 

2. At relatively high temperature, O2  obeys the equation of state :

 

                                             

 

 

a) Explain why this EOS is accurate at higher temperatures.

 

b) Show that for a reversible adiabatic expansion of this gas from (T1,V1) to (T2,V2) that:

 

                                                  

 

c) Obtain an expression for the final temperature in terms of P1, P2 and the initial

    temperature, T1.

 

 

 

 

3. Using the fact that U can be written as a function of P, T or V,T:   i.e

     U= U(P,T) or  U=U(V,T),  and that V=V(P,T):

 

a) Use the rules for total differentials to show that:

 

                                    

 b) Use U=H-PV to obtain an expression for Cp-Cv in terms of and .

c) Show Cp-Cv= nR for an ideal gas.

 

 

  4. The Joule-Thompson coefficient is written as:

 

                       

 

 

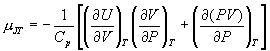
a)     Use this to show that the coefficient for an ideal gas is zero

b)     What does this mean physically?

 

5.                               

 

a) If q(V,T), what would be true about the second order derivatives of q if was an exact differential?

 

b) We have said in class that  is not an exact differential. Use (a) to show that  is not an exact differential for an ideal gas.

 

 

6. Two moles of ideal gas are expanded isothermally and irreversibly from 20 to 30 liters against a constant external pressure. The total work for the process is –5.065 kJ.

a)     Determine the external pressure.

b)     Evaluate  DU,  DH and q for the process

c)     If the system is at equilibrium at the end, what is the temperature?

 

 

7. Two moles of an ideal gas at 500K and 10 atm are in an insulated cylinder with a movable piston:

 

 

 

 


The gas is allowed to expand reversibly and adiabatically by introducing more gas into the cylinder at the current instantaneous temperature through an inlet valve. The internal pressure is maintained at a constant 10 atm throughout the expansion. The total work at the end of the process is –50 Latm. Calculate the final temperature of the gas inside the cylinder, and determine the number of moles of gas present in the cylinder.